Black Belt Story

Non, ce paradoxe n’a aucun rapport avec la famille déjantée que nous connaissons tous. Il s’agit plutôt d’une bizarrerie statistique permettant des interprétations totalement fausses et pouvant aboutir à des décisions prises de bonne foi, mais infondées.

Le paradoxe de Simpson est en effet simple à comprendre, et cependant têtu, coriace, et résistant à ce que nous appelons ordinairement le « bon sens ».

Prenons un exemple. Deux usines (1 et 2) fabriquent deux sortes de produits (A et B). Comme dans toute fabrication, il y a des défauts constatés, des rebuts. Les usines ayant démarré depuis quelques semaines, les taux de rebuts sont donc encore très importants.

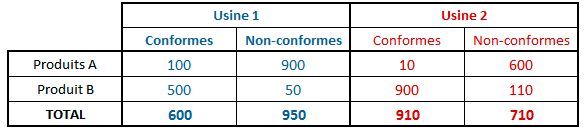
On a ainsi, pour chaque usine, le nombre de produits A conformes et non-conformes. Même chose pour le produit B. Les résultats se présentent ainsi :

Pour frapper davantage les esprits, représentons graphiquement cette situation.

Projetons-nous dans l’espace feutré d’une salle de comité de Direction, avec cette présentation. Chacun commente ses résultats. Le Directeur Général, qui supervise les 2 usines, regarde les résultats dans leur ensemble, c’est-à-dire la ligne TOTAL, et que constate t-il ? Que le taux de produits conformes est bien supérieur dans l’usine 2.

En effet, l’usine 2 fait apparaitre un taux de produits conformes de 910 / (710 + 910), soit 56%. L’usine 1, quant à elle, présente un taux de 600 / (950 + 600) soit 39% seulement. Le Directeur général blâme donc le directeur de l’usine 1, pour ses résultats piteux.

Le Directeur de l’usine 1, blessé dans son orgueil professionnel, fait alors remarquer que son taux de conformité du Produit A est supérieur à celui de l’usine 2. En effet,ce taux est de 100/(900 + 100) soit 10%, là où celui de l’usine 2 est de 10 / (600+10), soit 2%, seulement…

De plus, il affirme que la prédominance de l’usine 1 sur l’usine 2 est totale, puisque le même phénomène se constate aussi sur le produit B. Le taux de conformité de l’usine 1 sur le produit B est de 500 / (500 + 50) = 91%, alors que celui de l’usine 2 est de 900 / (900+110) = 89%

En résumé, l’usine 1 est meilleure que l’usine 2, aussi bien sur le produit A que sur le produit B, mais est moins bonne que l’usine 2 quand on regarde les totaux ! Comment se fait-il que l’usine 2 réussisse globalement mieux que l’usine 1 alors que c’est l’inverse pour chaque ligne de produits ?

Cela vient du fait que si les productions totales sont comparables (environ 1600 produits dans chaque usine), les pourcentages entre produit A et produit B sont très différents par usine. L’usine 1 produit 35% de produits B alors que l’usine 2 en produit 51%. Or, le produit B semble beaucoup plus facile à fabriquer, puisque le taux de rebut du produit B est d’environ 10%, quelle que soit l’usine.

Il est donc tout à fait exact de dire :
– L’usine 1 a un meilleur taux de conformités que l’usine B, quel que soit le produit
et
– Globalement, l’usine 1 présente de moins bons taux de conformités que l’usine B

Le paradoxe réside donc dans notre incapacité à accepter que quelque chose soit vrai partout, de façon locale, mais faux globalement ! et pourtant, c’est le cas. Ne concluons pas trop vite, sur la seule base de données globales…

Et merci à M. Simpson.